In our previous article Machine Learning: An Introduction to CART Decision Trees in Ruby opens a new window , we covered CART decision trees and built a simple tree of our own. Decision trees are very flexible and are a good tool for simple classification, but they are often not enough when it comes to real-world scenarios.

When dealing with large and complex data, or when dealing with data with a significant amount of noise, we need something more powerful. That’s where ensemble models come into play. Ensemble models combine a number of weak learners to build a strong model, with increased accuracy and robustness. Ensembles also help manage and reduce bias and overfitting.

In this article, we’ll cover a very popular tree-based ensemble model: Random Forest.

Introduction

Ensemble models are a pretty powerful technique. Conceptually, they can be built with any kind of weak learner, and can handle both regression and classification (binary or multi-class) tasks.

A weak learner is a model that is only slightly better than random choice. Considering a binary classification problem, if you pick a class at random for a particular instance, you have a 50% chance of being right. Weak learners are only slightly better than that.

For the purposes of this article, we’ll focus on a specific type of weak learner: decision trees. It is important to note that decision trees are weak learners when shallow and, in ensemble models, trees are kept intentionally shallow. A standalone tree can be a strong learner if allowed to grow complex enough.

We’ll also focus on a specific type of problem, the one applicable to the use case described in our Machine Learning Aided Time Tracking Review: A Business Case article opens a new window , binary classification.

Brief Introduction to Random Forest Classification

Random Forests operate by constructing multiple decision trees, pooling the class prediction outputted by each individual tree and choosing the class with the most votes (mode) as the final prediction to output.

A few interesting concepts to know when dealing with Random Forests:

Bootstrapping: a statistical resampling technique that involves, in the context of Random Forests, creating multiple subsets of the original training dataset by drawing each subset randomly with replacement; that is, after each draw, the selected item is put back into the original set and can be picked up again. This means that at the end of the process, each tree gets a subset of data, and different subsets might have repeating data points.

Bagging: Bagging, short for Bootstrap Aggregating, is an ensemble technique that trains multiple weak learners (which, in the case of Random Forest, are individual decision trees) independently on different bootstrap samples and then aggregates their predictions to produce a final prediction.

The combination of bootstrapping and bagging is what helps reduce variance in the model, allowing for more robust and accurate models. It ensures each tree in the group is different, which is crucial for the team of trees to work well together and deal with complicated patterns in data. As an added plus, since each tree can be trained independently, Random Forests are highly parallelizable, making them efficient on large datasets.

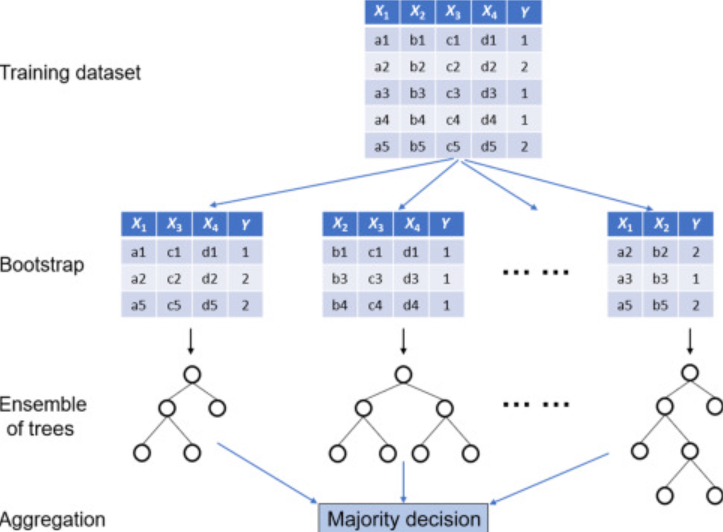
Implementation of a Random Forest classifier. Source: Machine Learning for Subsurface Characterization by Siddharth Misra and Hao Li

Random Forest Classifier Algorithm

Random Forest classification works by training multiple individual trees and taking the individual predictions to arrive at a final one. One key difference to keep in mind is that decision trees constructed by a Random Forest classifier are constructed from bootstrap-sampled data, not from the total dataset.

To construct the trees, multiple subsets of the original data are created via bootstrapping. These subsets will compose the root node of each tree.

For classification, as you may recall from the previous article on CART decision trees opens a new window , Gini impurity is used to define the feature and threshold to split on, with the goal being to always minimise impurity in the set. It is also possible to use Information Gain to split the dataset, but in this article we’ll focus on Gini impurity.

At each split, a random subset of features is chosen, with the best split being found within this subset. In standard implementations of Random Forest, including Scikit-learn’s opens a new window , the sample is the same size as the original dataset, but the composition of features and instances will vary. The randomness aspect increases the diversity of the trees, helping make the model more robust and reducing overfitting.

Each tree in the forest yields a classification. Considering a forest with \(K\) trees, each yielding a prediction \(C_k(x)\) of the Kth tree for input x, the final prediction is:

Where mode refers to the most frequent class label among all the class labels predicted by the individual trees in the forest.

Building a Random Forest Classifier

Now that we have a good understanding of Random Forests, let’s leverage our DecisionTree class from the previous article and build a very simple RandomForestClassifier of our own.

Like with the DecisionTree, we want a train method and a predict method. The difference is the train method of the classifier will call the DecisionTree’s train method on a random subset of the original data.

First, we’ll initialize a couple of things we’ll need: the number of trees to construct and the maximum depth of each tree. We’ll need to store the trees in an array.

def initialize(n_trees, max_depth)
  @n_trees = n_trees
  @max_depth = max_depth
  @trees = []
end

In order to train the individual trees, we’ll need bootstrapped samples. Let’s define a private method to randomly select samples from the original dataset that we can use to train the trees:

def bootstrap_sample(data, labels)
  bootstrapped_data = []
  bootstrapped_labels = []
  n_samples = data.length

  n_samples.times do 
    index = rand(n_samples) 
    bootstrapped_data << data[index]
    bootstrapped_labels << labels[index]
  end

  [bootstrapped_data, bootstrapped_labels]
end

Now we can build our train method. All it needs to do is, for as many times as the number of trees defined, train a DecisionTree on a bootstrapped sample, and store the tree in the array of trees:

def train(data, labels)
  @n_trees.times do 
    tree = DecisionTree.new
    bootstrapped_data, bootstrapped_labels = bootstrap_sample(data, labels)
    tree.train(bootstrapped_data, bootstrapped_labels, @max_depth)
    @trees << tree
  end
end

Finally, for the prediction, our predict method needs to gather individual predictions for each one of the trees and return the mode of those predictions:

def predict(sample)
  predictions = @trees.map { |tree| tree.predict(sample, nil) }.compact
  return nil if predictions.empty?
  predictions.group_by(&:itself).values.max_by(&:size).first
end

Putting it all together, we have a simple Random Forest Classifier:

require_relative "decision_tree"

class RandomForestClassifier
  attr_accessor :n_trees, :max_depth, :trees
  
  def initialize(n_trees, max_depth)
    @n_trees = n_trees
    @max_depth = max_depth
    @trees = []
  end

  def train(data, labels)
    @n_trees.times do
      tree = DecisionTree.new
      bootstrapped_data, bootstrapped_labels = bootstrap_sample(data, labels)
      tree.train(bootstrapped_data, bootstrapped_labels, @max_depth)
      @trees << tree
    end
  end

  def predict(sample)
    predictions = @trees.map { |tree| tree.predict(sample, nil) }.compact
    return nil if predictions.empty?
    predictions.group_by(&:itself).values.max_by(&:size).first
  end
  
  private

  def bootstrap_sample(data, labels)
    bootstrapped_data = []
    bootstrapped_labels = []
    n_samples = data.length

    n_samples.times do
      index = rand(n_samples)
      bootstrapped_data << data[index]
      bootstrapped_labels << labels[index]
    end

    [bootstrapped_data, bootstrapped_labels]
  end
end

We’re all set! We now have a very simple Random Forest Classifier of our own. Of course, for actual use cases, we need a much more robust algorithm, which is why we used Scikit-learn (and thus Python) to build our own. The goal of this demonstration is to explain the basic concepts behind how the classification works.

It’s also important to note that, as of the writing of this article, there wasn’t necessarily an “equivalent” to Scikit-learn in Ruby in terms of robustness and maturity of the platform. The rumale gem opens a new window does a great job of implementing Random Forest in Ruby, but given the other aspects of the process, including data processing, encoding, visualization, among others, we decided to use Scikit-learn on our implementation.

For more information on Scikit-learn’s implementation of Random Forests, check out their documentation opens a new window .

Conclusion

First, we built our very own decision tree. Now, we have made our model more robust by building an ensemble model, our very own Random Forest. This kind of algorithm is quite popular and widely used in a variety of different machine learning applications.

As you can imagine, though, there are situations where Random Forest’s voting approach is not the best. Random Forests sometimes struggle with very complex decision boundaries or highly imbalanced datasets, they may not significantly reduce bias as individual decision trees might have high bias, and errors might compound as trees are built independently. Gradient Boosting is a different ensemble model technique that aims to help with some of these limitations by trying to correct the errors of previous trees with each new tree. Next in this series, we’ll look at Gradient Boosting Classifiers and how they do that.

Excited to explore the world of Machine Learning and how it can be integrated into your application? We’re passionate about building interesting, valuable products for companies just like yours! Send us a message over at OmbuLabs! opens a new window !